序贯相似性检测算法(SSDA)
传统的模板匹配算法的基本搜索策略是遍历性的,为了找到最优匹配点,传统方法均必须在搜索区域内的每一个像素点上进行区域相关匹配计算,图像相关匹配的数据量和计算量很大,匹配速度较慢,序贯相似性检测算法(SSDA)是针对传统模板匹配算法提出的一种高效的图像匹配算法。具体算法是先初步搜索,再精搜索,搜索的范围一步一步减小。
思路
SSDA通过人为设定一个固定阈值,及早地终止在不匹配位置上的计算,以此减小计算量,达到提高运算速度的目的。其步骤如下:
(1)选取一个误差准则,作为终止不匹配点计算的标准,通常可选取绝对误差
(2)设定一个不变阈值
(3)在子图象中随机选取一点,计算它与模板中相应点的绝对误差值, 将每一随机点对的误差累加起来,若累加到第r次时误差超过设定阈值,则停止累加,记下此时的累加次数r
(4) 对于整 幅图像计算误差e,可得到一个由r值构成的曲面,曲面最大值处对应的位置即为模板最佳匹配位置。这是因为该点需要多次累加误差才能超过阈值,因此相对于其它点,它最有可能是匹配位置。
推导
假设:S(x,y)是MxN的搜索图,T(x,y)是mxn的模板图,是搜索图中的一个子图(左上角起始位置为(i,j))。则存在
SSDA算法描述如下:
①定义绝对误差:
其中,带有上划线的分别表示子图、模板的均值:
实际上,绝对误差就是子图与模板图各自去掉其均值后,对应位置之差的绝对值。
②设定阈值Th;
③在模板图中随机选取不重复的像素点,计算与当前子图的绝对误差,将误差累加,当误差累加值超过了Th时,记下累加次数H,所有子图的累加次数H用一个表R(i,j)来表示。SSDA检测定义为:
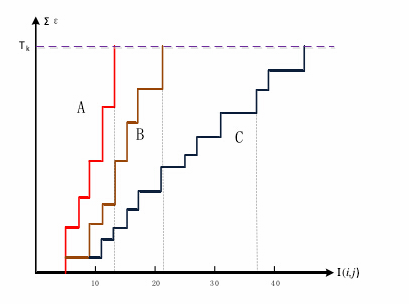
下图给出了A、B、C三点的误差累计增长曲线,其中A、B两点偏离模板,误差增长得快;C点增长缓慢,说明很可能是匹配点(图中Tk相当于上述的Th,即阈值;I(i,j)相当于上述R(i,j),即累加次数)。
④在计算过程中,随机点的累加误差和超过了阈值(记录累加次数H)后,则放弃当前子图转而对下一个子图进行计算。遍历完所有子图后,选取最大R值所对应的(i,j)子图作为匹配图像【若R存在多个最大值(一般不存在),则取累加误差最小的作为匹配图像】。
由于随机点累加值超过阈值Th后便结束当前子图的计算,所以不需要计算子图所有像素,大大提高了算法速度;为进一步提高速度,可以先进行粗配准,即:隔行、隔离的选取子图,用上述算法进行粗糙的定位,然后再对定位到的子图,用同样的方法求其8个邻域子图的最大R值作为最终配准图像。这样可以有效的减少子图个数,减少计算量,提高计算速度。
 支付宝
支付宝  微信
微信